前言
在了解GPUImage2 中GaussianBlur的实现与优化之前需要读者先了解如下图形知识:
- 卷积。卷积相关的基础可参考这篇理解图像卷积的意义。
- 高斯模糊算法。高斯模糊是基于高斯函数的权重分布,生成的卷积核。可先阅读这篇高斯模糊算法。
- 二阶高斯线性可分,属于常见的实现上会用到的一个理论点。可以参考二维卷积分为一阶卷积
具备了这些前提知识后我们就可以来看,GPUImage2的高斯模糊算法,以及作者实现中的优化了。本文所用的变量名称都是源码中的变量名称。
GPUImage2中的GaussianBlur实现
顶点与片段着色器配置流程与优化
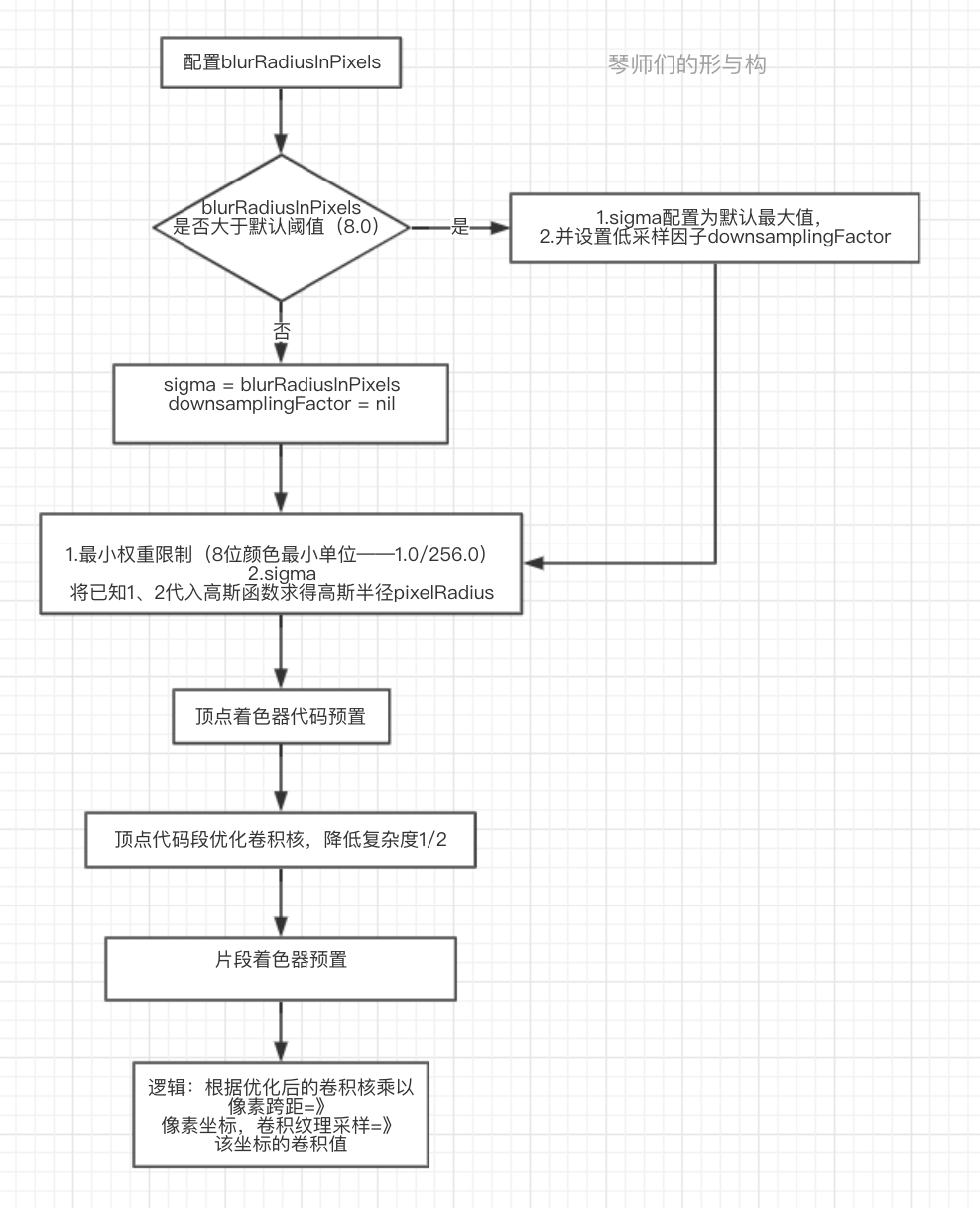
GPUImage2里面的GaussianBlur实现流程中包含了一些实现优化。顶点片段着色器算法配置实现的大概流程如下图:
 流程概述:
流程概述:
- 初始化后可以设置 blurRadiusInPixels (可以理解为配置的粗略的模糊半径)。实现体中如果 blurRadiusInPixels大于 8.0,将产生另外一个值 downsamplingFactor (即降低采样率因子)并使sigma = 8.0;可以理解为如果配置的模糊半径比较大,则会产生一个降低采样因子 downsamplingFactor = round(blurRadiusInPixels)/8.0。
- 生成程序中符合条件的卷积半径。首先设定最小权重值为1.0 / 256.0(对于8位颜色通道来说,小于该值的权重算是没有意义的);将最小权重值,sigma,代入高斯函数中求出卷积半径 pixelRadius。
- 卷积核数组优化。
- 根据已生成的 pixelRadius 与 sigma 代入高斯函数生成标准的卷积核数组。
- 根据标准卷积数组生成优化卷积数组。标准的卷积数组对应如:0:a(0);1:a(1);2:a(2);3:a(3);4:a(4);5:a(5);… n:a(n); 优化后的卷积数组,像素位置与权重对照如:0:a(0);1+(a(1)/(a0+a1):a(1); 3+(a(3)/(a2+a3):a(2); … 2x-1+(a(x)/(a(x-1)+a(x)):a(x/2+1);其中 x = (n%2+n/2)。 卷积核优化来看,复杂度从O(n) -> O(n/2);
- 由于优化后的卷积核的pixel 坐标都是非整数 2x-1+(a(x)/(a(x-1)+a(x)),所以优化后的卷积坐标都需要乘以源纹理的像素跨距(1/size.height or 1/size.width)获取到特定的计算卷积的纹理坐标。
渲染纹理流程
 流程概述:
流程概述:
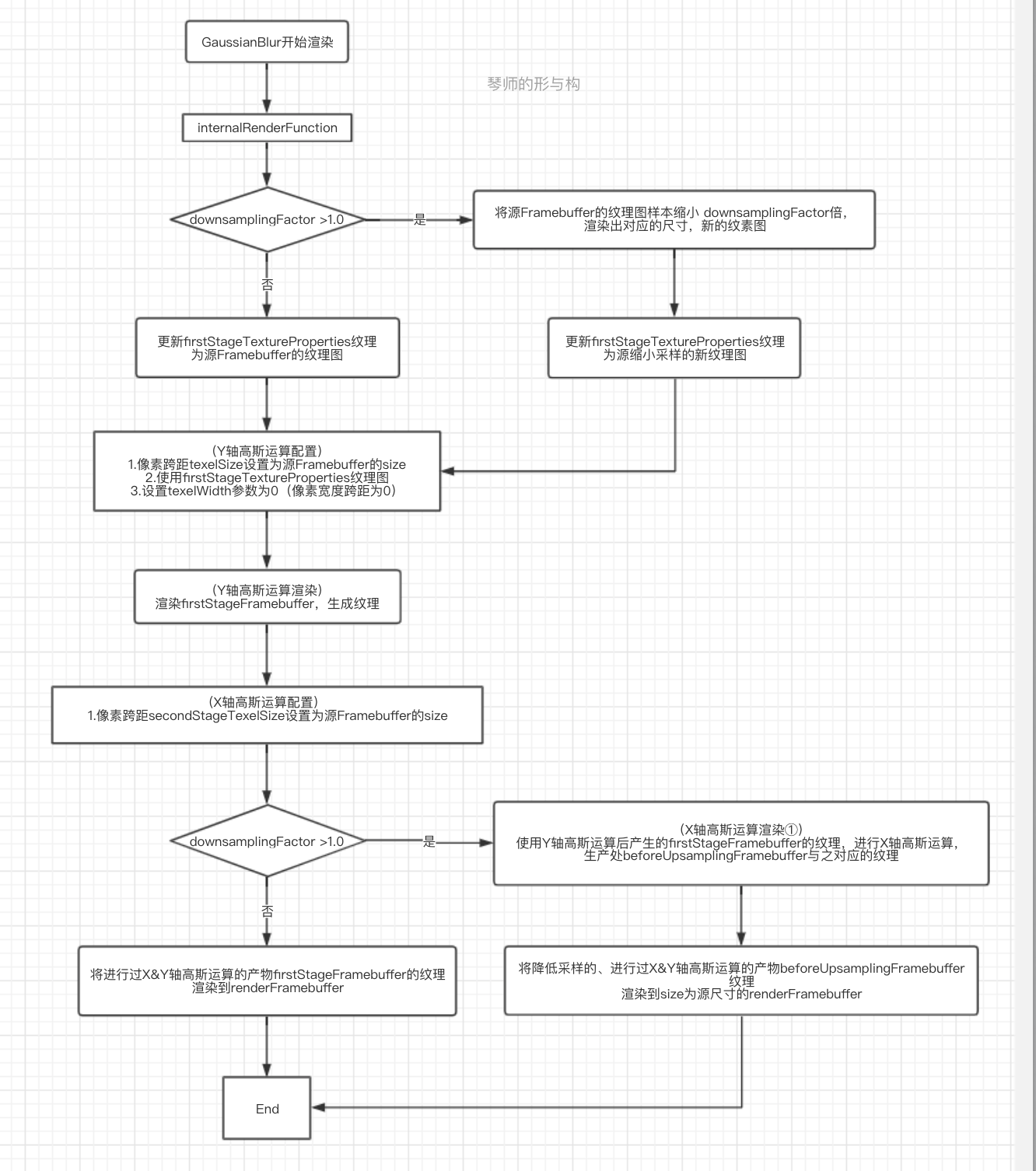
根据二阶高斯线性可分性,将渲染流程主要分成了Y轴高斯计算,X轴高斯计算。即牺牲空间复杂度,降低时间复杂度。
有一种特殊情况,即初始设定的模糊半径大于阈值时候(blurRadiusInPixels>8.0)。此时将会对图片进行降低采样等特定纹理处理如下:
- 先对源纹理低采样,生成新的纹理(低采样后的纹理)。
- 对低采样纹理进行Y轴高斯计算生成新的纹理。
- 对第2步产生的纹理进行X轴高斯计算生成新的纹理。
- 使用3步骤生成的纹理,渲染到源纹理尺寸目标frameBuffer,生成与源纹理尺寸一致的纹理。